You can tackle many tricky geometry questions with a single word ‘Construction’. Yes, just precisely draw the diagram as asked in the question and manually measure the unknown side/angle that has been asked…
Disclaimer: Use this method only when you are unable to figure out how to solve a question.
Q. 1) If BE and CF are two medians of a triangle ABC and G is the centroid and EF and AG intersects each other at O then find – AO:OG
(A) 1:1 (B) 1:2 (C) 2:1 (D) 3:1
Since no information about the type of triangle is given, hence we will assume it to be ‘Equilateral’.
Step 1: Draw an Equilateral triangle of any size(but it should be big enough for the purpose). Take 6 cm.
How to draw an equilateral triangle? Just draw a line AB = 6 cm, and make ∠A = 60 and ∠B = 60, the point where the two angles will intersect, will be point C.
Step 2: Now draw the medians BE and CF. Make sure that E and F lie exactly in the middle of AC and AB respectively.
Step 3: Complete the remaining figure.
Step 4: Measure AO and OG with a ruler.
You will find that AO:OG = 3:1
Answer: (D)
Again, a simple question.
Step 1: Draw a circle of any radius with centre O and diameter AB.
Step 2: Put protractor at A and draw ∠CAB = 34.
Step 3: Join BC
Step 4: Measure ∠CBA with protractor.
Answer: (C)
This may appear tricky if you go on solving it with conventional methods. But it is way too easy when solved through construction.
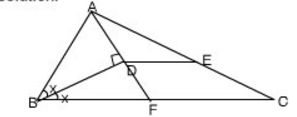
Step 1: Draw a triangle ABC with AC = 6 cm. Here we are using the concept of scaling. In the exam you can’t draw a line 12 cm long. Hence we are reducing AC to 1/2. Hence, when we will measure AE, we will have to multiply it by 2 to get the exact answer.
Step 2: Draw internal bisector of ∠ABC. Now, be very cautious, a slight mis-measurement give you a wrong answer. Use protractor for accurate measurements (For simplicity, you can take ∠A = 60 and hence use protractor to make ∠CBD = 30)
Step 3: Again with the help protractor, make ∠BDA = 90
Step 4: Draw DE parallel to BC
Step 5: Measure AE with a scale. You will get AE = 3 cm.
Hence actual length of AE = 2*3 = 6 cm
Answer: (B)
Method:
AD extended meets BC at F.
∠ADB = ∠BDF = 90
∠ADB = ∠FDB (BD is the angle bisector)
∠BAD = ∠BFD
Triangles ABD and FBD are congruent. So AD = DF
Triangles ADE and AFC are similar
AE/AC = AD/AF = 1/2
AE = 1/2 * 12 = 6 cm
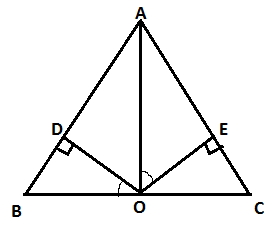
Q. 4)
Although this is a very simple question and you would get 60 degrees as your answer when you solve it. But, if by any chance, if you are not able to figure out the method, solve it using construction.
Method: The median of an isosceles triangle cuts the opposite side at right angles. Hence ∠AOB = 90.
Similarly you can solve many geometry questions with proper measurements. Try solving some questions on your own…
