 For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
Quant Quiz On Pie Chart Day 8 Bag
Buy Quant & Reasoning Tricks Book – Buy Now
Example 1:

Answer the following questions with reference to the above pie chart
Q1. Of every dollar received by the federal government, how much (in cents) is from coporate sources?
A. 32
B. 70
C. 30
D. 35
E. 29
Answer : 1
Q2. what percentage of the federal revenue is derived from borrowings?
F. 0.2%
G. 0.02%
H. 2.7%
I. 1.2%
J. 2.5%
Answer : 3
Example 2:
Chart 1 shows the distribution of twelve million tonnes of crude oil transport through different modes over a specific period of time. Chart 2 shows the distribution of the cost of transporting this crude oil. The total cost was Rs. 30 million.

1.What is the cost of transporting petroleum by rail (in Rs)?
1. 2.5
2. 3.33
3. 6.4
4. 8
2.If the cost per tonne of transport by ship, air and road are represented by P, Q and R respectively, which of the following is true?
1. R > Q > P
2. P > R > Q
3. P > Q > R
4. R > P > Q
3. The cost in rupees per tonne of oil moved by rails and happens to be roughly
1. 3
2. 1.5
3. 4.5
4. 8
4. From the charts given, it appears that the cheapest mode of transport is:
1. Road
2. Rail
3. Pipeline
4. Ship
5.Which is the most effective way of transportation?
1.Road
2. Ship
3. Pipeline
4. cannot be determined
6.If for some reason ship stop sailing, by what percentage the airfreight have to go up to reach the previous level of volume transported (approximately)?
1. 75%
2. 81%
3. 85%
4 .90%
If the revenue after selling the petroleum was Rs 40 Million and other costs (including oil extraction, marketing etc) is Rs 5 Million, answer the following.
7.What is the Profit percentage?
1. 10%
2. 12.5 %
3. 15%
4. 20%
8. If the cost of transportation rises by 20 % and so does revenue,what is the margin %?
1. 14.08
2. 14.28
3. 14.58
4. 14.78
9.If all costs rise by 10% and revenue remains same ,what would be the decrease in percentage profit?
1. 35
2. 50
3.70 4 .80
10. If the pipeline cost increases by 30% ,by what percentage would revenue have to be increased so as to have same amount of profit?
1. 11.5
2.12.8
3.13.75
4. 14.6
11. If the govt includes a 15% tax on transportation costs ,what would be the effective cost per tonne of petroleum so as to have the same amount of profit as before?
1. 3.2
2.3.5
3.3.7
4. 4.2
1. 2. We get 3.6/1.08=3.33
2. 3 Calculate the cost by ship, air and road.
P = 3/1.08 = 2.77; Q = 2.10/1.32 = 1.58; R = 1.80/2.64 = 0.68 hence P > Q > R
3. 1 3.60/1.08 = 3.33
4. 1 Road is the cheapest, from Q 132.
5. 4 cannot be determined as e do not know on what criteria
6. 2. Air freight is 11% .it would have to increase to 20% i.e. increase by 81.81%
7. 2. 12.5 %
8. 3. 14.58 profit of 7 Million on revenue of 48 Million
9. 3. 70 %
10.4. Pipeline cost is 65%ie 19.5 Million. If this rises by 30 %, it rises by 5.85 Million .to offset this, Revenue would have to rise by the same amount, so 100 = 14.625%
11. 3. 3.7
Example 3:

Answer the following questions with reference to the above pie chart
Q1. What fraction of Ghosh babu’s weight consists of muscular and skin proteins?
(a) 1/13
(b) 1/30
(c) 1/20
(d) Cannot be determined
Q2. Ratio of distribution of protein in muscle to the distribution of protein in skin is:
(a) 3 : 1
(b) 3 : 10
(c) 1 : 3
(d) 3(1/2): 1
Q3. What percent of Ghosh babu’s body weight is made up of skin?
(a)0.15
(b) 10
(c) 1.2
(d) Cannot be determined
Q4. In terms of total body weight, the portion of material other than water and protein is
closest to:
(a)3/20
(b)1/15
(c)85/100
(d) 1/20
ANSWERS 1.(c) 2.(a) 3.(d) 4.(a)
Example 4:
The following pie charts give the percentage distribution of different types of employees in different departments, A, B, C, D and E.

1. What was the difference in total number of people in department A in 1999 and 2000?
(1)840
(2) 400
(3) 440
(4) 240
2. In the case of which department was there a maximum variation between 1999 and 2000?
(1)E
(2)B
(3)D
(4) A
3. If 300 employees left in department B at the end of 1999, how many people joined in this department in 2000?
(1) 340
(2) 460 (3) 980
(4) 1360
4. The number of employees in department D in 2000 is how many times the number of employees in department E in 1999?
(1) 3.5
(2) 2.8
(3) 2.33
(4) 1.77
5. What is the percentage increase in the number of employees in department C in 1999- 2000?
(1) 2%
(2) 2.34%
(3) 23.45%
(4) None of these
6. If the average monthly salary of employees in department A in 1999 was Rs 4,000, what was the annual salary bill for department A in 1999?
(1) Rs 19 lakh
(2) Rs 19 crore
(3) Rs 22 crore
(4) Rs 22 lakh
7. If the average salary for the whole company remained same in 1999 and 2000 at the level of Rs.5,000 per month, what was the percentage increase in the salary bill for the company in the two years?
(1) 4%
(2) 8%
(3) 9%
(4) 11%
ANSWERS:
1. 1 22% (18000) – 24% (20,000)
2. 3 Visually, we see D has the maximum variation.
3. 4 26% (20,000) = 23% (18,000) + 300
4. 2 20% (20,000)/8% (18,000)
5. 3 18% (18,000) to 20% (20,000) = 23.45%
6. 2 22% (18,000) ï€¿ï€ 4000.
7. 4 (20 – 18)/18 = 11%
Set 1 : The various sections of the population are indicated below in the pie-chart. Study the pie-chart and answer the following questions:
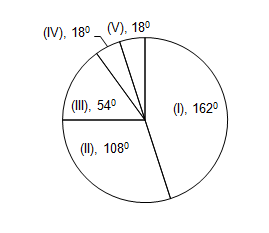
I. Employees of the Public Sector II. Employees of the Private Sector
III. Employees of the Corporate Sector IV. Self-Employed V. Unemployed.
1. What percentage of the employed persons is self employed?
| a. 5% | b. 5 5/19 % | c. 19% | d. 20% |
Solution: Total Employed = Total population – Unemployed = 3600−180=3420
Now self employed are 180. So self employed as a percentage of employed = 18342×100=5519%
2. Number of persons employed in the Corporate Sector is
| a. 250 | b. 500 | c. 750 | d. 1500 |
Solution: We have to convert degrees into numbers. So 54360×5000=750
3. The number of Unemployed persons is
| a. 250 | b. 150 | c. 100 | d. 50 |
Solution: We have to convert degrees into numbers. So 18360×5000=250
Shortcut: We calculated corporate sector employees as 750. But from pie chart Corporate sector employees are 3 times of unemployed. So 1/3rd of 750 = 250
4. The number of persons employed in both the Public Sector and Corporate Sector is
| a. 3750 | b. 3000 | c. 2500 | d. 2200 |
Solution: Number of persons employed in public sector and corporate sector together = 54 + 162 = 216.
54+162360×5000=216360×5000=3000
5. What percentage of the employed persons is employed in Private Sector ?
| a. 29% | b. 31 11/19% | c. 34% | d. 31% |
From the 1st question, employed are 342. and From pie chart private sector employees are 108.
108342×100=60019=311119%
1. What is the ratio between the number of appeared candidates from states C and E together and the appeared candidates from states A and F together ?
a. 17 : 33
b. 11 : 13
c. 13 : 27
d. 17 : 27
Solution: There is not need to calculate values. This is simply a ratio. So we can compare the ratio of their percentages. C + E = 8 + 9 = 17; A + F = 15 + 18 = 33.
So ratio = 17 : 33
2. In which State the percentage of qualified candidates to that of appeared candidates is minimum ?
Solution: This is a lengthy question. But we will use simple technique to solve this question.
We have to calculate the ratio of Qualified to appeared for each state. So
But If you observe in the above equation, only 18% / 15% changes for each state. Remaining values are constant. Minimum percentage we get if numerator is small and denominator is big.
For C it is 7/8 = 1/1.14 and for E it is 9/14 = 1/1.5 So for E denominator is big. So it has the ratio Minimum.
So Option D is correct.3. What is the difference between the number of qualified candidates of states D and G
| a. 690 | b. 670 | c. 780 | d. 720 |
Solution: Instead of calculating qualified candidates for D and G separately, we take the difference in their percentages. i.e., 8% (9000) = 720.
4. What is the percentage of qualified candidates to that of appeared candidates from states B and C taken together ?
| a. 23.11 | b. 24.21 | c. 21.24 | d. 23 |
Qualified candidates from B and C = (16 + 7)% = 23% (9000)
Appeared candidates from B and C = (11 + 8)% = 19% (45000)
So required percentage =
23%(9000)19%(45000)×100=2319×5×100=24.21
5. What is the ratio between number of candidates qualified from states B and D together and the number of candidates appeared from state C respectively ?
| a. 8 : 37 | b. 11 : 12 | c. 37 : 48 | d. 7 : 37 |
Solution: The required ration = (16 + 21)% (9000) : 8% (45000)
Example 1
Consider the information provided in the pie chart below relating to India’s foreign trade in 1997-98 and the first eight months of 1998-99. Total trade with a region is defined as the sum of exports to and imports from that region.
Trade deficit is defined as the excess of imports over exports. Trade deficit may be negative.

Example 1.A
What is the region with which India had highest total trade in 1997-98?
(A) USA (B) Other E.U. (C) OPEC (D) Others
Answer – (C)
Solution:
Trade with a region is the aggregate of imports from and exports to that region. The question is about a relative position and not an absolute position and thus should involve nothing more than glancing the pie charts and at the very most some small additions that can eminently he done orally. Whatever he the figures of total exports and total imports, these will not be necessary since what is asked is a relative position.
If we assume that the total exports is E and total imports is I, then in the case of USA, the imports will be 9I1009I100 and exports will be 19E10019E100 and in the case of Other E.U. imports will be 12I10012I100 and exports will be 14E10014E100. So when you are comparing (9I100+19E100)(9I100+19E100) with (12I100+14E100)(12I100+14E100), you can safely multiply both sides so as to get whole numbers such that now we shall be comparing (9I+19E)(9I+19E) with (12I+14E)(12I+14E).
In the present case, imports into India are USD 40779 million and we may safely take I as 4 (rounding off 40779 to the nearest ten thousand) and exports from India are USD 33979 million we may safely take E as 3 (rounding off 33979 to the nearest ten thousand).
Comparing (9I+19E)(9I+19E) with (12I+14E)(12I+14E) will mean comparing (9∗4+19∗3)(9∗4+19∗3) with (12∗4+14∗3)(12∗4+14∗3) and hence 93 with 90 and so India’s total trade with USA is more than the total trade with Other EUs. In evaluating the options, all that one has to do is to put the percentage of imports and if it is say 21% then write it as 21 and write the imports as 4 and so on. Now see the Options.
Option A: USA (9∗4+19∗3)=93(9∗4+19∗3)=93
Option B: Other EU (12∗4+14∗3)=90(12∗4+14∗3)=90
Option C: OPEC (23∗4+10∗3)=122(23∗4+10∗3)=122
Option D: Others (1∗4+1∗3)=7(1∗4+1∗3)=7
Option C is the clear choice. It would be stupid to merely add the percentages alone. A percentage is after all so much out of the whole. If you are comparing percentages of the same whole, you can tell which is higher. But comparing differing percentages of two different wholes is logical only when you take their absolute values. For Example 9% of 200 (we shall call 200 as A) is far higher than 36% of 40 (we shall call 40 as B) and rushing to the conclusion that 36% of B is higher than 9% of A would be stupid.
Assuming 40779 as 4 and 33979 as 3 would:
(A) Save a lot of time.
(B) Save a lot of effort..
(C) Ensure that we are comparing equals on both sides, and
(D) Ensure that you get the correct answer in a jiffy.
Example 1.B
In 1997-98 the amount of Indian exports, in millions US $, to the region with which India had the lowest total trade, is approximately:
(A) 750 (B) 340 (C) 220 (D) 440
Answer – (B)
Solution
Others occupy 1% of the pie in both imports and exports and is the area with the lowest total trade. Indian exports aggregate roughly 34000 million and 1% of this is two zeroes off from 34000 and would mean 340. Thus Option B.
Example 1.C
In I997-98, the trade deficit with respect to India, in billions of US $, for the region with the highest trade deficit with respect to India, is approximately equal to:
(A) 6.0 (B) 3.0 (C) 4.5 (D) 7.5
Answer – (A)
Solution:
Let us assume that total imports are 100I and total exports are 100E. In case of one region – Region 1 – the imports are A% and exports are B% and in region 2 imports are C% and exports are D%. Trade deficit in Region 1 is (AI−BE)(AI−BE) and in Region 2 it is (CI−DE)(CI−DE).
If Trade deficit in Region 1 is higher than in Region 2, then (AI−BE)−(CI−DE)(AI−BE)−(CI−DE) should yield a positive difference and this means that (AI−BE)>(CI−DE)(AI−BE)>(CI−DE). If you subtract CICI to both sides and add BEBE to both sides, you would get:
(AI−CI)>(BE−DE)(AI−CI)>(BE−DE) or I(A−C)>E(B−D)I(A−C)>E(B−D).
We know that I is greater than E in any case.
If (A−C)(A−C) is greater than (B−D)(B−D) the matter is clinched because then I(A−C)I(A−C) is indeed > E(B−D)E(B−D) and thus Trade deficit in Region 1> Trade deficit in Region 2.’
After all, (A−C)(A−C) is some number and (B−D)(B−D) is some other number. So (A−C)%(A−C)% of a higher base is bound to be higher than (B−D)%(B−D)% of a lower base so long as (A−C)>(B−D)(A−C)>(B−D). This is utter logic. This logic is what is at test here.
In the present case, in all regions except OPEC and other East Europe, exports percentages are either more than or equal to imports percentages. We have to thus compare only OPEC and other East Europe and see whether (Difference in percentages of imports)> (Difference in percentages of exports).
In the case of OPEC and other East Europe (Difference in percentages of imports)=(23−19)(23−19) and (Difference in percentages of exports)=(10−10)(10−10) and hence (Difference in percentages of imports)>(Difference in percentages of exports) and thus trade deficit in OPEC is highest.
The trade deficit in this case works out to (0.23∗41−0.1∗34)=9.2−3.4=5.8(0.23∗41−0.1∗34)=9.2−3.4=5.8 roughly.
Thus Option A: 6 billion.
Example 1.D
What is the region with the lowest trade deficit with India in 1997 – 98?
(A) USA (B) Asia (C) Others (D) Other E.U.
Answer – (A)
Solution:
The lowest trade deficit can also means a negative trade deficit or trade surplus. In case of the earlier question we have seen that Other EU has the second highest trade deficit and thus it is not a likely candidate for the least trade deficit. Hence we cross out Option D.
In USA and Asia we have trade surplus. In case of others there is a deficit. When we have trade surpluses, then we are to ignore trade deficits because a trade surplus is a negative trade deficit. So Option C is to be crossed out as well. We are now left with Options 1 and 2.
As we have seen in the earlier question, if (Difference in percentages of imports) is greater than (Difference in percentages of exports) than Trade deficit in Region 1 > Trade deficit in Region 2. Now if we are to compare USA with Asia,
(Difference in percentages of imports) =(9−14)=−5=(9−14)=−5 and
(Difference in percentages of exports)=(19−20)=−1=(19−20)=−1.
Since -5 is not higher than -1, the trade deficit in USA is lower than the trade deficit in the case of Asia and hence Option A.
ADDITIONAL DIRECTIONS for Examples 1.E and 1.F: Those questions are based on the situation below:
Assume that the average monthly exports from India and imports to India during the remaining four months of 1998-99 would be the same as that for the first eight months of the year.
Example 1.E
What is the region to which Indian imports registered the highest percentage growth between 1997-98 and 1998-99?
(A) Other East Europe (B) USA (C) Asia (D) Exports have declined, no growth
Answer – (B)
Solution:
Look at the pie chart for exports in 1997-98, which is for a full year and for 1998 99, which is for eight months only.
As per the additional information, we are to assume that the average monthly exports from India and imports to India during the remaining four months of 1998-99 would be the same as that for the first eight months of the year.
If for eight months, the total exports have been 21436 million, the remaining four months (which is half of eight months) would have brought about an additional export equal to half of 21436 million, which is 10718 and the total exports would then have been 32154 million.
Since we are to state a comparative position – growth rate in exports in 1997-98 and exports in 1998-99, we can safely ignore the millions.
11% of 100 is less than 9% of 200 and so also 11% of I00 Billion is less than 9% of 200 Billion. What is the need for these millions while stating which is greater?
Secondly, if you are to compare between growth in exports over base yeah then you must appreciate that exports in 1998-99= exports in 1997-98 + growth in between/exports in 1997-98 = 1+ growth in between/exports in 1997-98 and thus when you compare the exports of two different regions, you can safely take the exports in the next year as a fraction of the base year instead of finding the difference between the exports in an year and the exports in the base year because when you compare the exports figures of Region 1 with that of Region 2 instead of incremental exports, you will get 1 on both sides of the comparison like this:
[1+ growth in between of exports in Region 1/exports in 1997-98] compared with [1+ growth in between of exports in Region 2/ exports in 1997-98], and if you strike off the 1 on both sides what you are really comparing is:
[Growth in between of exports in Region 1/exports in 1997-98] with [Growth in between of exports in Region 2/exports in 1997-98] which is what you want.
Let us see the options.
Option A:
Other East Europe. 10% of 33979 has grown to 12% of 32154. Let 1% of 33979 be A and 1% of 32154 be B. So in the case of Other East Europe, exports in 1998-99/exports in 1997-98 = 12B/10A.
Option B:
USA, 19% of 33979 has grown to 23% of 32154. Let 1% of 33979 be A and 1% of 32154 be B. So in the case of USA, exports in 1998-99/exports in 1997-98 = 23B/19A.
Option C:
Asia, 20% of 33979 has grown to 19% of 32154. Let 1% of 33979 be A and 1% of 32154 be B. So in the case of Asia, exports in 1998-99/exports in 1997-98 = 18B/20A.
Now what we are required to do is to compare among 12B/10A, 23B/19A and 18B/20A and say which is largest. In that case, neither B nor A in the numerator and denominator respectively are necessary because if you multiply all three fractions by A/B then you get 12/10, 23/19 and 18/20 and yet the relative values of the three fractious will remain unchanged.
If you were to multiply three fractions – say – 1/2, 2/3, and 3/4 by one million in the numerator and five million in the denominator, will it alter the fact that 3/4 (as it will seem after all the multiplications) will remain the largest and 1/2 the smallest of these three fractions? See for yourself. The three fractions will respectively seem like this: 1 million/10 million, 2 million/15 million and 3 million/20 million and yet the last will be the highest and the first will be the lowest.
So what you are then comparing is 12/10, 23/19 and 18/20 in which 18/20 will have to be booted out since it is less than 1 and then we are left with 12/10 and 23/19. If we divide 12 by 10, we get 1.2.
If we divide 23/19 we get 1.2 till the first decimal and have to carry on to the next decimal and hence we get 1.21. We stop here and declare that USA has highest growth among the three options and thus Option B is correct.
But there is a small googly here. Option D says that exports have declined or there has been no growth in any region. This has to be checked. We know that the highest percentage growth is in the case of USA. But percentage growth is about relative growth whereas the Option D talks about absolute growth. Whether there has been no growth or decline in absolute terms can be ascertained from only absolute figures.
Now see the utter logic in this. If this logic goes home, you will be saved a huge lot of calculations. Logic is the name of the game and even if it takes some time for this simple logic to register, it is recommended that you should absorb the fundamentals.
Since we know that in case of USA the percentage growth rate has been highest, we may just see whether there has been actual growth in this case (we shall choose the highest percentage growth rate to check because if there has not been absolute growth where the percentage growth is highest, then in cases of lower percentage growth, the likelihood of an absolute growth is zero).
In case of USA, export percentage grew from 19% of 33979 million to 23% of 32154 million. For determining whether there was growth, the millions are unnecessary once again. They would be needed if you were asked how much was the growth.
But even then, if the answer is to be given in millions, the millions become redundant once again. Give these millions a well-earned rest. Round off 33979 to 34 (forget the thousands as well) and round off 32154 to 32 (forget the thousands here as well) and see whether 19% of 34 is less than 23% of 32. You will find that so exports have indeed grown in the case of USA at least and hence Option D (which if true would mean that there has not been any growth in exports in any region) does not hold water.
So Option B.
Example 1.F
What is the percentage growth rate in India’s total trade deficit between 1997-98 and1998-99?
(A) 43% (B) 47% (C) 50% (D) 40%
Answer – (B)
Solution:
lndia’s trade deficit in 1997-98 in USD billions is:
40.7−33.9=6.840.7−33.9=6.8
In 1998-99, it is (28.1∗1.5)−(21.4∗1.5)=42.15−32.1=10.05(28.1∗1.5)−(21.4∗1.5)=42.15−32.1=10.05.
The trade deficit has gone up from 6.8 billion USD by 3.25 billion USD to 10.05.
This increase of 3.25 as a percentage of 6.8 is:
3.25∗1006.8=3256.83.25∗1006.8=3256.8
=325068=162534=325068=162534.
Now 34∗50=170034∗50=1700. 1625 is 75 less than 1700.
So 162534=50−(7534)162534=50−(7534).
But 75347534 is more than 2 and thus 162534162534 is likely to be more than 47 and less than 48.
From among the options 47% seems to be the answer. So Option B: 47%.













