How To Solve Simple Interest Shortcut Tricks & Tips

---

Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips : Fillers Short-Cut Tricks & Tips Question Pdf for Banking, SSC, RRB, FCI, Railway, UPSC, State PCS, Insurance & other Competitive exams. Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips shortcut Tricks Pdf, Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips MCQ, Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips Objective Question & Answer Pdf. “Fillers Short-Cut Tricks & Tips Questions PDF” In this post we are providing you the Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips pdf with detailed solution & Short Tricks. So that you can easily get the logic of question. This Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips Pdf we are Providing is free to download. ” Most Important Fillers Short-Cut Tricks & Tips Question PDF with Answers“

Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips Plays a vital role in Exam. In every exam you will get at least 5-10 questions from this topic. So candidates must focus on this topic and download this Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips pdf to get important questions with best solution regarding Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips. We have put all Previous Year Questions of Simple Interest(SI) & Compound Interest(CI) Short-Cut Tricks & Tips that are Asked in various Govt & Private Exam.

Definition of the term Interest: Interest is actually one of the most fundamental business terms, and without it, the financial trading of the world would come to standstill. Interest is defined as the “time value of money”.

What exactly does this mean?
Well, look at this way: with time, the value of money changes. Suppose you have Rs. 100 in the year 2000. Would it still be Rs. 100 or would the amount have grown? If you had deposited the money in a saving bank account, say with an annual rate of interest 4%, that money would have definitely grown by now. Can you calculate the amount you would have with you in 2013? Well, in case you can’t right now, go through these concept notes and you would know the answer.

The concept of simple and compound interest is especially applicable to the world of banking and economics. Whenever we borrow a certain sum of money (known as the principal), we pay back the original amount accompanied with a certain amount of interest on that amount. In a way, those are the charges of borrowing that sum of money. Simple interest is one method of determining the amount due at the end of loan duration. Another method of interest application is compound interest, but we study about it in next article.

Important Shortcut Tricks

 

Interest is the money paid by the borrow to the lender for the use of money lent.
The sum lent is called the Principal. Interest is usually calculated at the rate of so many rupees for every Rs.100 of the money lent for a year. This is called the rate per cent per annum.
‘Per annum’ means for a year. The words ‘per annum’ are sometimes omitted. Thus, 6 p.c. means that Rs.6 is the interest on Rs.100 in one year.
The sum of the principal and interest is called the amount. The interest is usually paid yearly, half-yearly or quarterly as agreed upon.
Interest is of two kind, Simple and Compound. When interest is calculated on the original principal for any length of time it is called simple interest. Compound interest is defined in the next chapter.

 

To find Simple Interest, multiply the principal by the number of years and by the rate per cent and divide the result by 100.

This may be remembered in the symbolic form

Where I = Interest, p = principle, t = number of years, r = % rate

Ex. 1. Find the simple interest on Rs.400 for 5 years at 6 per cent.

Solution:

Interest for a number of days

When the time is given in days or in years and days, 365 days are reckoned to a year. But when the time is given in months and days, 12 months are reckoned to a year and 30 days to the month. The day on which the money is paid back should be include be but not the day on which it is borrowed, ie, in counting, the first day is omitted.

Ex. 2. Find the simple interest on Rs.306. 25 from March 3^rd to July 27^that per annum.

Solution:

Interest = Rs. 

= = Rs. 4.59

To find principal:-

Since I =       

Ex.3. What sum of money will produce Rs.143 interest in  years at p.c. simple interest?

Solution:

Let the required sum be Rs. P. Then

Rs P = 

To find rate %:-

Since I =                              

 

Ex. 4. A sum of Rs.468.75 was lent out at simple interest and at the end of 1 year 8 months the total amount was Rs500. Find the rate of interest per cent annum.

Solution:

Here, P =Rs468.75, t = or 

I = Rs.(500-468.75) = Rs.31.25

rate p.c. = 

To find Time:-

Since, I = P t r / 100                        

Ex. 5. In what time will Rs.8500 amount to Rs.15767.50 at per cent per annum?

Solution:

Here , interest = Rs.15767.50 – Rs.8500 =Rs.7267.50

Miscellaneous Examples on Simple Interest:-

Ex.6: The simple interest on a sum of money is 1/9^th of the principal, and the number of years is equal to the rate per cent per annum. Find the rate per cent.

Solution:

Let principal = P, time = t year, rate = t

Then,                         

Hence, rate = %

Direct formula:

Rate = time = %

Ex. 7: The rate of interest for the first 2 yrs is 3% per annum, for the next 3 years is 8% per annum and for the period beyond 5 years 10% per annum.To fetch an interest of 1520 in six years, money did he deposit?

Solution

Let his deposit be = Rs 100

Interest for first 2 yrs = Rs 6

Interest for next 3 yrs = Rs 24

Interest for the last year = Rs 10

Total interest = Rs 40

When interest is Rs 40, deposited amount is Rs 100

when interest is Rs 1520, deposited amount = = Rs 3800

Direct formula:

Principle = Interest*100/r₁t₁+r₂t₂+r₃t₃… = =Rs 3800

 Ex.8: A sum of money doubles itself in 10 years at simple interest. What is the rate of interest?

Solution:

Let the sum be Rs 100

After 10 years it becomes Rs 200

Interest = 200 – 100 = 100

Then, rate =  = 

Direct formula:

Time × Rate = 100 (Multiple number of principal – 1)

Or, Rate = 

Using the above formula rate = 

Ex.9: A sum was put at a certain rate for 2 yrs. Had it been put at 3% higher rate, it would have fetched Rs 300 more. Find the sum.

Solution:

Let the sum be Rs x and the original rate be y% per annum. Then, new rate = (y+3) % per annum

xy +3x – xy =15,000 or, x =5000

Thus, the sum =Rs 5000

Gradestack Method : Direct Formula

Sum =  = 

Ex.10. The simple interest on a certain sum of money at 4% per annum for 4 yrs is Rs 80 more than the interest on the same sum for 3 yrs at 5% per annum. Find the sum.

Solution:

Let the sum be Rs.x , then, at 4% rate for 4 yrs the simple interest = = Rs.  

At 5% rate for 3 yrs the simple interest =  = Rs 

Now, we have,  or, 

Or,  x= Rs 8000

Gradestack Method : For this type of question

Sum =  = Rs 8000

 

Simple Interest Tool tip1: The Definitions
Principal (P): The original sum of money loaned/deposited. Also known as capital.
Interest (I): The amount of money that you pay to borrow money or the amount of money that you earn on a deposit.
Time (T): The duration for which the money is borrowed/deposited.
Rate of Interest (R): The percent of interest that you pay for money borrowed, or earn for money deposited

Simple Interest Tooltip 2: The Formula

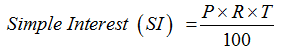
Where:
P: Principal (original amount)
R: Rate of Interest (in %)
T: Time period (yearly, half-yearly etc.)

Amount Due at the end of the time period, A = P (original amount) + SI

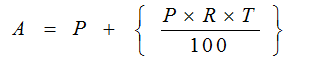
If you have a close look, Simple Interest is nothing else but an application of the concept of percentages.

Simple Interest Tooltip 3: Basic Problems to explain the concept

Basic Problem 1: What is the SI on Rs. 7500/- at the rate of 12% per annum for 8 years?

Using the Basic Formula:
Simple Interest (SI) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest

Given P = 7500, T = 8 Years, R = 12%
Simple Interest (S.I.) = (7500X12X8)/100
Simple Interest (S.I.) = 7200

Basic Problem 2: A man borrowed Rs 15000/- at the rate of 24% SI and to clear the debt after 6years, much he has to return:

Using the Basic Formula:
Simple Interest (SI) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest
Given P = 15000, T = 6 Years, R = 24%
Simple Interest (S.I.) = (15000X24X6)/100= Rs 21600
Therefore, total interest = 21600
Total repayment = S.I + Principal amount = 21600 + 15000 = Rs 36600

Basic Problem 3: A man borrowed Rs.12000 at the rate of 10% SI, and lent the same sum toanother person at the rate of 15% what will be the gain after 5 years?

Using the Basic Formula:
Simple Interest (S.I.) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest

The man borrowed at 10% and he lent the same sum to another person at 15%
Therefore, his gain is actually equal to the different in the interest rate (per year)
= 15 – 10 =5% for 1 year
Thus, to calculate his gain, we use this difference as the rate of interest.
Given T = 5 years and P = Rs. 12000
Amount Gained = (12000x5x5)/100 = Rs 3000
Therefore, his gain = Rs 3000/-

Suppose u deposit 100 Rs at Bank , having Rate of interest as 10% and After 1 Yr u need to calculate that what ll be the SI AND CI  ..

(1st Method Still a very TIME CONSUMING)..

If we go by Formulae

SI  = (PRT)/100

So SI ll be (100*10*1)/100 = 10   

And 

CI = P{(1+ R/100)^n -1}

    =  100 {(1+ 10/100)^1    –       1}

   =  100 (1.1 – 1) 

   = 10

This Basically leads to The CONCLUSION that for 1st YR SI AND CI ll remain the same..

 

2nd Method 

Basically i ll be using here the Percentage concept .. 

Suppose u need to calculate the SI for 100 Rs at 10% for 2 yrs..

1st thing is u can apply formulae here.

OR OR..

Rate for SI ll be same for every Year hence for 2 yr it ll be 10*2 = 20%

100 of 20%  is = 20  directly..

Same Question what  if its CI.

Applying formula ll surely take time…

Use this 

INTEREST FOR CI LL BE for 2 Yrs =(a + b + ab/100 )    where a and b are rate percent…

for 10% it ll be = (10+ 10 + 100/100) = 21%

Now again from percentage concept we ve

21% of 100  = 21

 

 Another method For CI ll be 

100 of 10% = 10

So net Amount ll be after 1st Yr = 100+10  = 110

     

Net amount for  110 of 10% = (110+ 11)   = 121

hence Interest ll be (121 – 100 )  = 21

 

NOW SOME TPYES OF QUESTION WHICH IS GENERALLY ASKED…  THESE ARE IMPORTANT IF U RE A BEGINNER…

 

TYPE 1 …

Principal Needs to be calculated when DIFFERENCE BETWEEN CI AND SI is given as Some AMOUNT . let ur say it is A.. and Rate of Interest is R… and say TIME IS 2 years…

Let A be 10

R = 10% and Time = 2 Yrs..

Formulae ll be 

Principal =   Difference Amount  (100/Rate)^2

Principal be than = 10 (100/10)^2   = Rs.  1000

U can go by the basic method but i guess that ll be a kind of CRIME if u re appearing In COMEPETITIVE EXAMINATION…   😛

 

TYPE 2…

What if i reverse the Question..

Now u know Principal amount , rate and Time …

Principal =   Difference Amount  (100/Rate)^2

Now using the same formula u can calculate the Interest

Question ll be like 

Principal is Rs 100

Rate is 10% and Time is 2 yrs..

Difference ll be ?????

Apply Formula

100 = x  (100/10)^2

hence x = 1     (I guess its Easy to understand)…

Another Method For this Question can be applied only if u re STRONG in ur PERCENTAGE SECTION

SI ll be 100 of 20% = 20

CI ll be 100  of 21% = 21    (Formula used is A+ B + AB/100) 

Hence

CI  MINUS SI ll be 21 – 20 = 1  (Same as Above) 

 

TYPE 3….

Suppose u need to calculate WHAT LL BE CI OR SI When ONE them is given..

and we know TIME , RATE  nd INTEREST…

Question ll be like 

Suppose CI is known as 210 and rate is 10% for 2 yr . What ll be its SI ..?

Apply the Formula

{(200 + Rate)/200} = (CI/SI)

(200+10/200) =  (210/x)

hence x = 200

Lets change the data now , CI is 1050 .. Rate is 10% and time is 2 years..

(200+10)/200   = 1050/SI

hence SI ll be  1000

 

TYPE 4…

The sum of money doubles itself in 5yr. In how many years it becomes 8 times the initial.

Let initial be 100 hence final ll be 800

1^st method

Net yr = 5+ 5 + 5 = 15 Yr..

2nd method

Time 2 / Time 1 = Power 2/ Power 1

Power ll be always in the form of 2..

Time 1  =  5 Yrs 

Time 2 = ?? 

Power 1 = 2^1  (Doubles Given)

Power 2  = 8 times  = 2^3

hence from Formula we ve 

Time 2/ Time 1 (5) =  3/1

Time 2 = 3*5 = 15 Yrs…

 

Type 5…

First Power / Time 1   = Second Power / Time 2

If sum of money gets 4 times in 3 yrs , than when it ll become 6 times..

As far as here the power is concerned i ve taken it as a multiple of 2…

ie 2 is 2 times of 4

nd 2 is 3 times of 6

2/3 = N/6

hence N = 4 times

 

Simple Interest Tips, Tricks, and Results: Tooltip 1

If the interest on a sum of money is 1/x  of the principal, and the number of years is equal to the rate of interest then rate can be calculated using the formula: √(100/x)

Derivation for this result:
We Know SI = {(P x R x T)/100}
Put SI = P/x  ; and T=R
P/x = {(P x R x T)/100}
R² = 100/x
R = √(100/x)

Example : The interest on a sum of money is 1/16 of the principal, and the number of years is equal to the rate of interest. What is the rate percent?

Solution :

Using the above concept :

R = √(100/x)

R = √(100/16)

R = 5/2%

Simple Interest Tips, Tricks and Results: Tooltip 2

The rate of interest for t₁ years is r₁% , t₂ years is r₁%, t₂ years is r₃ %.If a man gets interest of Rs x

for (t₁+ t₂ + t₃ =n)  years, then principal is given by

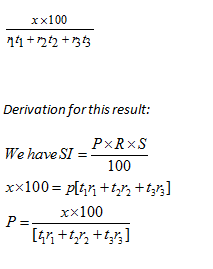
Example: The rate of interest for 3 years is 4%, 5years is 6%,1 years is 5%. If a man gets interest of Rs. 4700 for 9 years, calculate the principal amount?

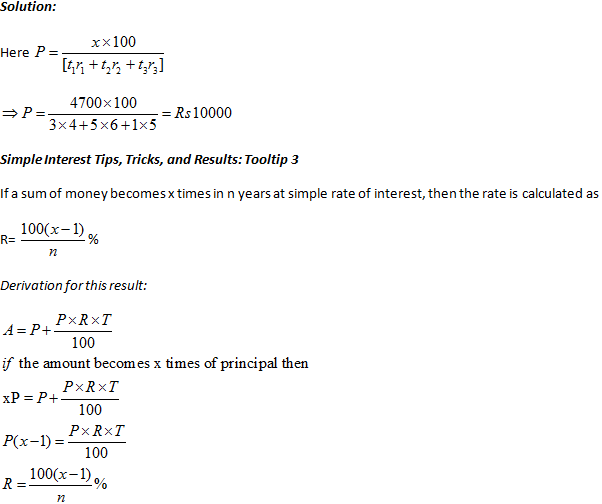
Example: A sum of money becomes 4 times in 20 years. Calculate the rate of interest.

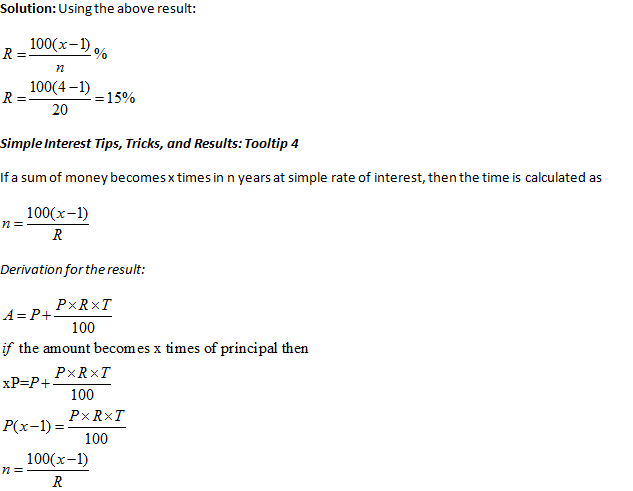
Example: A sum of money becomes 4 times in 20 years. Calculate the rate of interest.

Solution:

Using the above result:

R = [{100(x-1)}/n]%

R = [{100(4-1)}/20]=15%

Simple Interest Tips, Tricks, and Results: Tooltip 4

If a sum of money becomes x times in n years at simple rate of interest, then the time is calculated as

n= {100(x-1)/R}

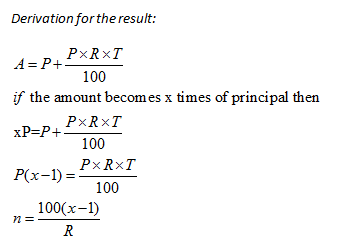
Example:A sum was put at SI at a certain rate for 3 years. If the sum would have put at a 2% higher rate, it would have yieldedRs 900 more. What will be the principal?

Solution:

Use the above formula:

P= {100X/(nX r)}

P= {(900 x 100)/(3 x2)} = Rs. 15000

This tooltip is a reverse of the last one. A sum is put at SI at a certain rate for n years. If the sum would have put at a r% lower rate, it could yield Rs X less. So the principal will be:

P= {100X/(n * r)}

Example: A sum was put at SI at a certain rate for 3 years. If the sum would have put at a 2% lower rate, it could yield Rs 900 less. What will be the principal?

Solution:

Using the formula, we arrive at the following:

P= {100X/(n * r)}

P= {(900*100)/(3*2)}

P = Rs. 15000

 

Tips, Tricks& Results for Simple Interest-2

The purpose of this article is to provide you with some useful tips and tricks that you can use for Simple Interest questions. Various applications and formulas based on this concept are explained here.

Simple Interest Tips, Tricks, and Results: Tooltip 1

Change in Simple Interest when time changes from T₁ to T₂ is given by the formula:

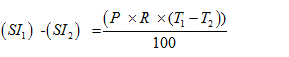
Change in Simple Interest when principal changes from P₁ to P₂  is given by the formula:

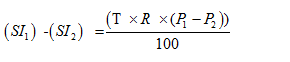
Change in Simple Interest When rate of interest changes from r₁to r₂ is given by the formula:

Example: Simple interest on Rs 200 increases by Rs 50 when time increases by 5 years. Find rate percent per annum.

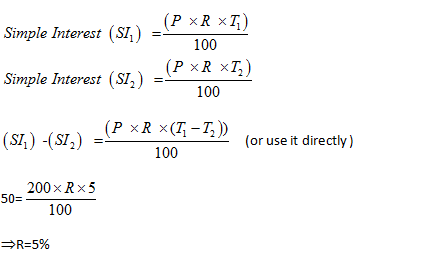
Example: If the SI on Rs 1000 be more than the interest on 2000 by Rs 20 in 4 years, find the rate per annum.

Solution: When principal changes from  P₁to P₂

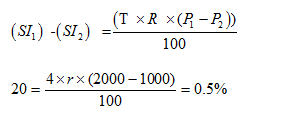
Simple Interest Tips, Tricks, and Results: Tooltip 2

If a person deposits A₁  amount at r₁% per annum and amount A₂ at r₂% per annum, then the rate of interest for the whole sum is {(A₁r₁ + A₂r₂)/(A₁+A₂)}

Example: A man deposits Rs.1000 at 4% per annum and Rs 2000 at 5% per annum, find the rate of interest for the whole sum.

Solution: 
Method-1:
Using the formula for, Simple Interest (SI) =  {(P x R x T)/100}
X = {(1000 x 4 x 1)/100} = 40
Y = (2000 x 5 x 1)/100 = 100
Total interest = 100+40=Rs. 140
Total principal =1000+2000=Rs.3000
Using the formula:
140 = {(3000 x R x 1)/100}
R = 14/3%

Method-2:
Applying above concept {(A₁r₁ + A₂r₂)/(A₁+A₂)} , the rate of interest is
[{(1000 x 4) + (2000 x 5)}/(1000 + 2000)]
= 14000/3000
14/3%

Simple Interest Tips, Tricks, and Results: Tooltip 3
A certain amount is invested for certain time but at different rates. When rate per annum is r₁ the amount becomes x₁ but at rate  r₂ per annum, the amount becomes x₂ .
Time, t, is given by the formula:
t = {(x₁ – x₂)/(x₂r₁ – x₁r₂)}*100

 

Simple Interest (SI)

If the interest on a sum borrowed for certain period is calculated uniformly, it is called simple interest(SI). (fix percentage of principal)

What is Principal (sum)

Principal (or the sum) is the money borrowed or lent out for a certain period. It is denoted by P.

What is Amount?

The Addition of Simple Interest and Principle is called the Amount.

A = S.I + P ( Principle )

Interest

Interest is the extra money paid by the borrower to the owner (lender) as a form of compensation for the use of the money borrowed calculated on the basis of Principle.

Time

This is the duration for which money is lend / borrowed.

Rate of Interest

It is the rate at which the interest is charge on principal.

What is Per annum means?

“Rate of interest R%  per annum” means that the interest for one year on a sum. If not stated explicitly, rate of interest is assumed to be for one year.

Formulas Need to Remember

S.I =[( P X R X T )/( 100 )].

Where P = Principle, R = Rate of per annul, T = Number of years

From the above formula , we can derive the followings

P=(100×SI)/ RT

R=(100×SI)/ PT

T=(100×SI)/ PR

Some Tricks to Solve easily

Trick 1:- If a sum of money becomes “n” times in “T years” at simple interest, then the rate of interest per annum can be given be

Trick 2:- If an amount P1 is lent out at simple interest of R1% per annum and another amount P2 at simple interest rate of R2% per annum, then the rate of interest for the whole sum can be given by

Trick 3:- A sum of money at simple interest n1 itself in t1 year. It will become n2 times of itself in (If Rate is constant)

 

Trick 4:- In what time will the simple interest be “n” of the principal at “r %” per annum:-

rt =n x 100

 Trick 5:- If a certain sum of money is lent out in n parts in such a manner that equal sum of money is obtained at simple interest on each part where interest rates are R1, R2, … , Rn respectively and time periods are T1, T2, … , Tn respectively, then the ratio in which the sum will be divided in n parts can be given by

How To Solve Compound Interest Shortcut Tricks & Tips

Compound Interest :- Sometimes it so happens that the borrower and the lender agree to fix up a certain unit of time, say yearly or half-yearly or quarterly to settle the precious account.

In such cases, the amount after first unit of times becomes the principal for the second unit the amount after second unit becomes the principle for the third unit and so on.

After a specified period, the difference between the amount and the money borrowed is called the Compound Interest (abbreviated as C.I.) for that period.

 

Compound Interest is the interest calculated on the initial principal and the accumulated interest of previous periods of a deposit or loan.

In easy words, it can be said as “interest on interest”. It makes a deposit or loan grow faster as compared to simple interest. The interest at which compound interest accumulates depends on the frequency of compounding; more the number of compounding periods, the greater the compound interest.

Note: The interest for the first month is same in both Simple Interest and Compound Interest. From second month, the interest starts changing.

The formula for Compound Amount

P [1+ R/100]ⁿ [When money is compounded annually]
= P [1+ R/(2*100)]²ⁿ [When money is compounded half-yearly]
= P [1+ R/(12*100)]¹²ⁿ [When money is compounded monthly]
Also, A = CI + P
Where,
P= Principal
R= Rate of Interest
n=Time (in years)
A= Amount
CI= Compound Interest

Note: The above formula: A = CI + P will give us total amount. To get the Compound Interest only, we need to subtract the Principal from the Amount.

The table given below lists the values of an initial investment, P = Re. 1 for certain time periods and rates of interest, calculated at both, simple and compound interest. If memorized this would be of great help in time management during the exam,

Rate⇒ Time⇓	5%			10%			15%			20%
	SI	CI	Diff	SI	CI	Diff	SI	CI	Diff	SI	CI	Diff
1 year	1.05	1.05	0	1.1	1.1	0	1.2	1.2	0	1.2	1.2	0
2 years	1.10	1.1025	0.0025	1.2	1.21	0.01	1.4	1.44	0.04	1.6	1.69	0.09
3 years	1.15	1.1575	0.0075	1.3	1.331	0.031	1.6	1.728	0.128	1.9	2.197	0.297

To understand the above discussed concepts, let’s try some questions.

 

Solved Questions

Questions 1:Find the amount if Rs 20000 is invested at 10% p.a. for 3 years.

Solution: Using the formula_A= P [1+ R/100]ⁿ
A = 20000 [1 + (10/100)]³
On Solving, we get A = Rs. 26620

 

Question 2: Find the CI, if Rs 1000 was invested for 1.5 years at 20% p.a. compounded half yearly.

Solution: As it is said that the interest is compounded half yearly. So, the rate of interest will be halved and time will be doubled.

CI = P [1+(R/100)]ⁿ – P
CI = 1000 [1+(10/100)]³– 1000
On Solving, we get
CI = Rs. 331

Question 3: The CI on a sum of Rs 625 in 2 years is Rs 51. Find the rate of interest.

Solution: We know that A = CI + P
A = 625 + 51 = 676
Now going by the formula: A = P [1+(R/100)]ⁿ
676 = 625 [1+(R/100)]²
676/625 = [1+(R/100)]²
We can see that 676 is the square of 26 and 625 is the square of 25
Therefore, (26/25)² = [1+(R/100)]²
26/25 = [1+(R/100)]
26/25 – 1 = R/100
On solving, R = 4%

 

Question 4:A sum of money is put on CI for 2 years at 20%. It would fetch Rs 482 more if the interest is payable half yearly than if it were payable yearly. Find the sum.

Solution: Let the Principal = Rs 100
When compounded annually,
A = 100 [1+20/100]²
When compounded half yearly,
A = 100[1+10/100]⁴
Difference, 146.41 – 144 = 2.41
If difference is 2.41, then Principal = Rs 100
If difference is 482, then Principal = 100/2.41 × 482
P = Rs 20000.

 

Question 5: Manish invested a sum of money at CI. It amounted to Rs 2420 in 2 years and Rs 2662 in 3 years. Find the rate percent per annum.

Solution: Last year interest = 2662 – 2420 = Rs 242
Therefore, Rate% = (242 * 100)/(2420 * 1)
R% = 10%
Important Formula: To find the difference between SI and CI for 2 years, we use the formula Difference = P[R/100]²

 

Question 6:The difference between SI and CI for 2 years @ 20% per annum is Rs 8. What is the principal?

Solution: Using the formula: Difference = P (R/100)²
8 = P[20/100]²
On Solving, P = Rs 200

 

We all know the traditional formula to compute compound interest.

CI = P*(1+R/100)^N – P

This calculation gets very tedious when N>2 (more than 2 years). The method suggested below is a very simple way to get CI/Amount after ‘N’ years.

You need to recall the old Pascal’s Triangle in following way:

 

Code:

Number of Years (N)

——————-

1                        1

2                    1   2   1

3                  1   3   3   1

4                1   4   6   4   1

.              1 …. …. … … …. …   1

Example: P = 1000, R=10 %, and N=3 years. What is CI & Amount?

Step 1: 10% of 1000 = 100, Again 10% of 100 = 10 and 10% of 10 = 1

We did this three times becoz N=3.

Step 2:

Now Amount after 3 years = 1 * 1000 + 3 * 100 + 3 * 10 + 1 * 1 = Rs.1331/-

The co-efficients – 1,3,3,1 are lifted from the pascal’s triangle above.

Step 3:

CI after 3 years = 3*100 + 3*10 + 3*1 = Rs.331/- (leaving out first term in step 2)

If N =2, we would have had, Amt = 1 * 1000 + 2 * 100 + 1 * 10 = Rs. 1210/-

CI = 2 * 100 + 1* 10 = Rs. 210/-

This method is extendable for any ‘N’ and it avoids calculations involving higher powers on ‘N’ altogether!

A variant to this short cut can be applied to find depreciating value of some property. (Example, A property worth 100,000 depreciates by 10% every year, find its value after ‘N’ years).

N.B Prefer this method if N>=3. It will always work and it will save your time like anything.

 

Shortcuts for Calculating Compound Interest

Here is a shortcut trick for calculation of compound interest for 2 and 3 years. Instead of putting formulas and doing long calculation you can use the short tricks according to given percentage

CI for 2 Years                                                                                   CI For 3 Years

2%	4.04%	2%	6.12%
3%	6.09%	3%	9.27
4%	8.16%	4%	12.48
5%	10.25%	5%	15.76
6%	12.36%	6%	19.10
7%	14.49&	7%	22.50
8%	16.64%	8%	25.97
9%	18.81%	9%	29.50
10%	21%	10%	33.10
11%	23.21%	11%	36.76
12%	25.44%	12%	40.49
13%	27.69	13%	44.28
14%	29.96	14%	48.15
15%	32.25	15%	52.08
16%	34.56	16%	56.08
17%	36.89	17%	60.16
18%	39.24	18%	64.30
19%	41.61	19%	68.51
20%	44.00	20%	72.80

 

Some important formula of Compound Interest

• A = Amount.
  P = Principal.
  R = Rate of Interest.
  N = Number of Years.

 

• Type I : Interest compounded yearly : 
  A = P ( 1 + r / 100 )ⁿ
  

 

• Type II : Interest compounded half – yearly :
  Amount = P [ 1 + r / 2 / 100 ]⁴ⁿ or = P = [ 1 + r / 200 ] ²ⁿ

 

• Type III : Interest compounded quarterly :
  Amount = P [ 1 + r / 4 / 100 ] or = P [ 1 + r / 400 ] ⁴ⁿ

In Compound Interest problems asked in exams up to the period of 3 years.
In case we apply basic formula: Amount =Principal ( 1 + r / 100 )ⁿ here r = Rate and n = Time
As consider if Principal is Rs. 1, then the it will be in first year and second and third years.
( 1 + r / 100 )¹
( 1 + r / 100 )²
( 1 + r / 100 )³
If the rate of interest is 3%, then the value will be …….
In first year = (23 / 21 ) = 23 / 21.
In second year = ( 23 / 21 )² = 529 / 441.
In Third year = ( 23 / 21 )³ = 12167 / 9261.

 

Compound Interest Tricks: Results related to Multiple Compounding in a year:

In each of the following results, we use the following denotations:
A = future value
P = principal amount (initial investment)
r = annual nominal interest rate
n = number of times the interest is compounded per year
t = number of years for which the money is borrowed

Compound Interest Trick 1: If interest is not compounded yearly then

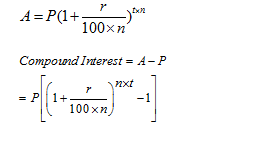
where

n= number of times compounding is done
if compounding is done half yearly then n = 2
if compounding is done quarterly  then n = 4
when compounded monthly then n=12

Amount for Half Yearly Compounding, A = P {1+(R/2)/ 100}^2T
(compound interest applied two times in a year)
Like Half Yearly Compound Interest, we can calculate the amount for Quarterly Compounding.
Amount for Quarterly Compounding,A = P {1+(R/4)/ 100}^4T

Example 1: Sona deposited Rs. 4000 in a bank for 2 years at 5% p.a.rate. Find the amount received by her from the bank if interest is compounded half yearly.

Solution: 
Principal value = Rs. 4000
Rate = 5%
Time = 2 years
Since the interest is compounded half yearly so 2 years = 4 times in two years
So, we have
A = P {1+(R/2)/ 100}^2T
A= 4000{1+ (5/2)/100}⁴
A = 4000 x 41/40 x 41/40 x 41/40 x 41/40
A = Rs. 4415.25
So, Sona received Rs. 4415.25 from the bank after two years

Example 2: Manpreet lent Rs 5000 to Richa at 10% rate for 1 year. But she told her that she will take her money on compound interest. Find the amount of interest received by Manpreet when compounded quarterly.

Solution: 
Principal value = Rs. 5000
Rate = 10%
Time = 1 year
The interest is compounded quarterly, that is 4 times in 1 year.
We use the formula=A = P {1+(R/4)/ 100}^4T
A= 5000{1+ (10/4)/100}⁴
A = 5000 x 41/40 x 41/40 x 41/40 x 41/40
A = Rs. 5519.064
So, Manpreet received Rs. 5519.064 from Richa and the total amount of interest received by her is 5519.064 – 5000 = Rs. 519.06

Compound Interest Tricks: When the rate % is not same for every year and interest is taken on yearly basis then amount can be calculated as:

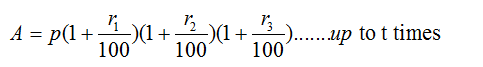
Example 3:  Find the compound interest on 16000 in 2 years , while rate of interest at first year is 3% and for the second year is 4%.

Solution: 

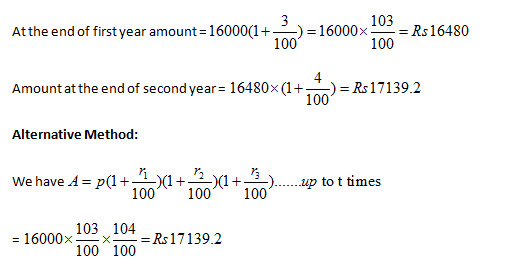
Compound Interest Tricks: When interest is compounded yearly and time is given in fraction

If time is given in mixed fraction

Use formula,

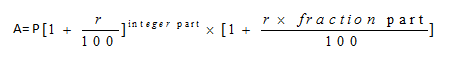
Example 4: The compound interest on Rs. 8,000 at 15% per annum for 2 years 4 months, compounded annually is:

Solution:

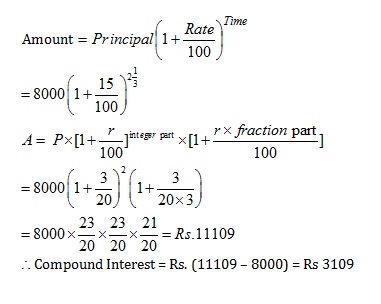
Compound Interest Tricks: Practice Questions

Question 1: A certain sum, invested at 4% per annum compound interest, compounded half – yearly, amounts to Rs 7,803 at the end of one year. The sum is

A. Rs 7,000
B. Rs 7,200
C. Rs 7,500
D. Rs 7,700

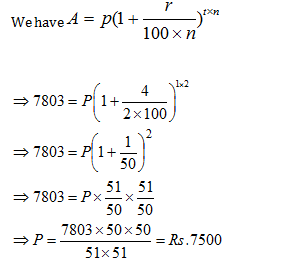
Question 2: If the rate of interest be 4% per annum for first year, 5% per an­num for second year and 6% per annum for third year, then the compound interest of Rs. 10,000 for 3 years will be

A. Rs. 1,600
B. Rs. 1,625.80
C. Rs. 1,575.20
D. Rs. 2,000

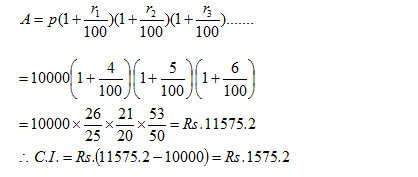
Question 3: The compound interest on Rs. 16,000 for 9 months at 20% per annum, interest being com­pounded quarterly, is

A. Rs. 2,520
B. Rs. 2,524
C. Rs. 2,522
D. Rs. 2,518

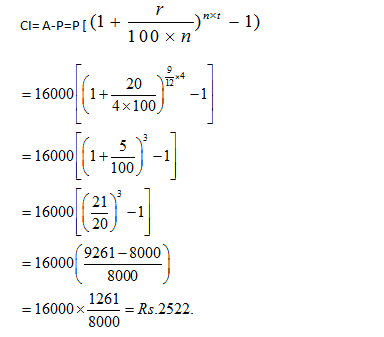
Question 4: The compound interest on Rs. 6,000 at 10% per annum for 3/2 years, when the interest be¬ing compounded annually, is
A. Rs. 930
B. Rs. 870
C. Rs. 910
D. Rs. 900

 

 

 

 

 

 

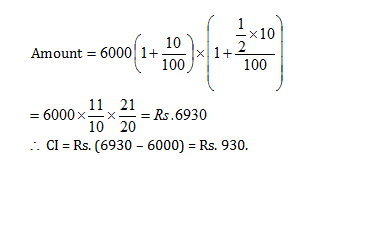
It is best to be selective with these compound interest shortcuts and use them to the best of your ability.

In each of the following results, we use the following denotations:

A = future value
P = principal amount (initial investment)
r = annual nominal interest rate
n = number of times the interest is compounded per year
t = number of years for which the money is borrowed

Let’s get started and cover some of these shortcuts.

Compound Interest Shortcuts: Tooltip-1

A sum of money placed at compound interest becomes x time in ‘a’ years and y times in ‘b’ years. These two sums can be related by the following formula:

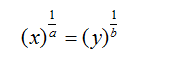
Derivation for this result:
We use the basic formula for calculating Compound Interest:

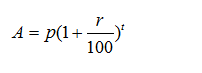
For condition 1, a sum of money becomes x times in “a” years.
Therefore, using the formula for calculating Compound Interest:

Example-1: A sum of money placed at compound interest doubles itself in 4 years.In how many years will it amount to 16 times itself?

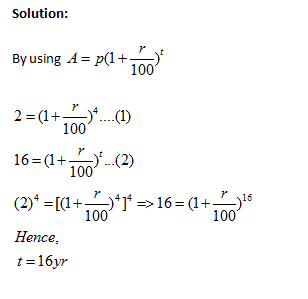
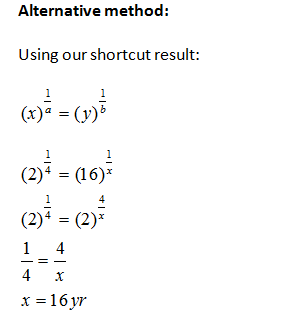
Compound Interest Shortcuts: Tooltip 2

If an amount of money grows up to Rs x in t years and up to Rs y in (t+1) years on compound interest, then

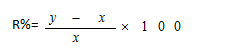
Derivation for this result:

Principal + CI for t years = x ……   (1)
Principal + CI for (t+1) years= y  …….  (2)
(2) – (1) =>CI for last year = y-x
Which is basically the simple interest upon x

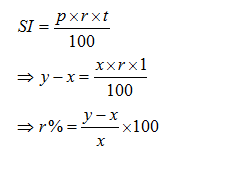
Example-2: An amount of money grows upto Rs 3000 in 3 years and upto Rs 4000 in 4 years on compound interest. What will be the rate percent?

Solution:
Principal + CI for 3 years = 3000 ……   (1)
Principal + CI for 4 years= 4000  …….  (2)
Hence (2) – (1) =>CI for 4th year = 4000-3000= Rs 1000
Which is basically the simple interest upon 3000

 

 

 

 

 

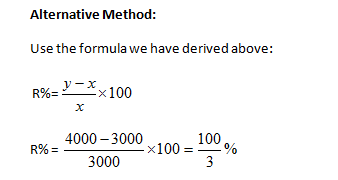
Compound Interest Shortcuts: Tooltip 3

A sum at a rate of interest compounded yearly becomes Rs. A₁ in n years and Rs. A₂ in (n + 1) years, then 

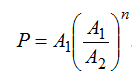
Example-3: A sum of money invested at compound interest amounts to Rs. 100 at the end of first year and Rs. 120 at the end of second year. The sum of money is :

Solution:
Simple Interest for one year = compound interest for one year
Interest on Rs. 100 for 1 year = 120-100= Rs. 20

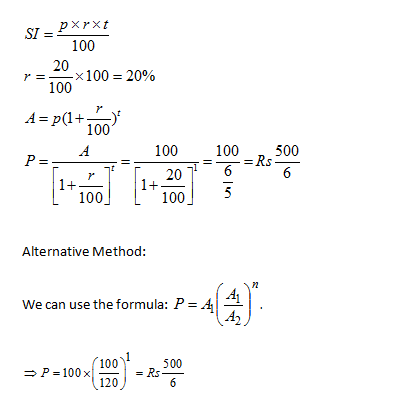
Compound Interest Shortcut: Tooltip 4

If a certain sum becomes x times of itself in t years, the rate of compound interest will be equal to

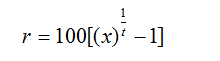
Derivation for this result:

Use the formula for Compound Interest Calculation:

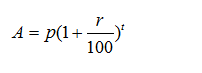
Sum becomes x times of itself in t years so

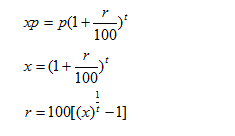
Example 4:  If a certain sum becomes 16 times in 2 years ,what will be the rate of compound interest?

Solution:

Using the formula derived above:

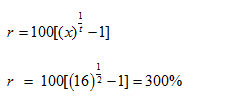
Compound Interest Shortcut: Tooltip 5If the compound interest on a certain sum for 2 years is CI and simple interest for two years is SI ,then rate of interest per annum  is

If the compound interest on a certain sum for 2 years is CI and simple interest for two years is SI ,then rate of interest per annum  is

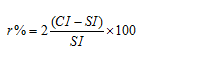
Derivation for this result:

Example 5: If the compound interest on a certain sum for 2 years is 20rs and simple interest for two years is 10rs  ,then what wil be the  rate of interest per annum  ?

Solution:

Using the formula derived above:

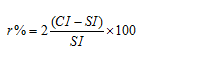
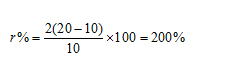
Compound Interest Solved Problems using Compound Interest Shortcuts:

Let’s go through some compound interest solved problems and learn how to use and implement compound interest shortcuts in actual problem solving. Remember, till the time you actually solve questions using these tricks, you won’t be able to memorize and understand them. Go through compound interest solved problems and hone your skills for the topic.

Question 1: What sum of money at com­pound interest will amount to Rs. 650 at the end of the first year and Rs. 676 at the end of the second year?

A. Rs. 600
B. Rs. 600.25
C. Rs. 625
D. Rs. 625.25

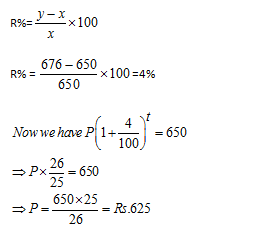
Question 2: If the amount is 2.25 times of the sum after 2 years at com­pound interest (compound annu­ally) , the rate of interest per an­num is :

A. 25%
B. 30%
C. 45%
D. 50%

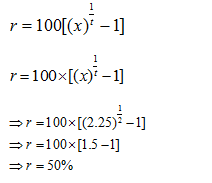
Question 3: A sum of money doubles itself in 4 years at compound interest. It will amount to 8 times itself at the same rate of interest in:

A. 18 years
B. 12 years
C. 16 years
D. 24 years

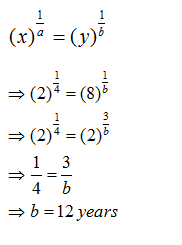
Question 4: A sum borrowed under com­pound interest doubles itself in 10 years. When will it become fourfold of itself at the same rate of interest?

A. 15 years
B. 20 years
C. 24 years
D. 40 years

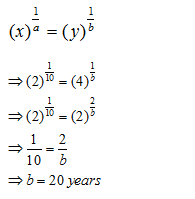
Question 5: A sum of money becomes eight times of itself in 3 years at com­pound interest. The rate of interest per annum is

A. 100%
B. 80%
C. 20%
D. 10%

 

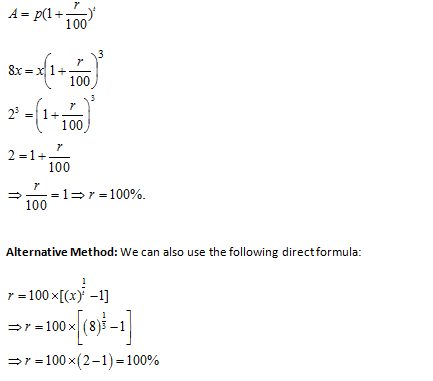
Important Facts & Formulas on Compound Interest

Case 1: Let principle = P, time = n years and rate = r% per annum and let A be the total amount at the end of n years, then

Example: Albert invested an amount of Rs.8000 in a fixed deposit scheme for 2 years at compound interest rate 5 p.c.p.a. how much amount will Albert get on maturity of the fixed deposit.

Solution: 

Amount = Rs.

= 8820 Rs.

Case 2: When compound interest is reckoned half-yearly.

If the annual rate is r% per annum and is to be calculated for n years, then in this case, rate = (n/2%) half-yearly and time = (2n) half-yearly.

Form the above we get

Example: Sam investment Rs.15,000 @ 10% per annum for one year. If the interest is compounded half-yearly, then the amount received by Sam at the end of the year will be.

Solution:

P = Rs. 15000; R = 10% p.a = 5% half-year, T = 1 year = 2 half year

Amount = Rs

= Rs.16537.50

Case 3: When compound interest is reckoned quarterly.

In this case, rate = (r/4%) quarterly and time = (4n) quarter years.

As before,

Example:

Find the compound interest on Rs. 15,625 for 9 months at 16% per annum compounded quarterly.

Solution:

P = Rs. 15625, n= 9 months = 3 quarters, R = 16% p.a. = 4% per quarter.

Amount = Rs.

= Rs.17576 —> C.I = Rs. (17576 – 15625 ) = Rs. 1951.

Note: The difference between the compound interest and the simple interest over two years is given by

{(Pr^2)/100^2}  or  {P (R/100)^2}

Case 4: When interest is compounded annually but time is in fraction, say  years.

Amount =

Example:

What is the difference between the compound interest on Rs. 5000 for  at 4% per annum compounded yearly and half-yearly?

Solutions:

C.I. when interest is compounded yearly .

= Rs.5304

C.I. when interest is compounded half-yearly

Difference = Rs.(5306.04 – 5304 ) = Rs.2.04.

Case 5: when rates are different for different years, say  for 1^st, 2^nd, 3^rdyear respectively.

Then, amount =

Example:

The population of Jhumri Tilaiya increases by 10% in the first year, it increase by 20% in the second year and due to mass exodus, it decreases by 5% in the third year. What will be its population after 3 years, if today it is 200,000?

Solution:

Population at the end of 1 year will be 10,000 + 10% of 10,000= 11,000

At the end of second year it will be 11,000 + 20% of 11,000 = 13,200

At the end of third year it will be 13,200 – 5% of 13, 20  = 12,540

Case 6: Present worth of Rs.x due n years hence is given by:

Present Worth = [x/{1+(r/100)^n}]

Example:

The principle that amounts to Rs.4913 in 3 years at  per annum compound interest compounded annually, is :

Solution:

Principle = Rs.

Q. 1) If a sum of money becomes 3 times itself in 20 years at simple interest. What is the rate of interest?
In such questions apply the direct formula-
Rate of interest = [100*(Multiple factor – 1)]/T
So R = 100*(3 – 1)/20
Answer : 10%
Note : With this formula you can find Rate if Time is given and Time if rate is given.

Q. 2) 

In such questions, just write this line :
1st part : 2nd part : 3rd part = 1/(100+T1 * r) : 1/(100+T2 * r) : 1/(100+T3 * r)
= 1/(100+2 * 5) : 1/(100+3 * 5) : 1/(100+4*5)
= 1/110 : 1/115 : 1/120
= 23*24 : 22*24 : 23*22
Hence 1st part = (23*24)/ (23*24 + 22*24 + 23*22) * 2379
Answer : 828
Note : Surprisingly, such questions when asked mostly have this same data, i.e., R=5% and T1, T2, T3 = 2, 3, 4 years, respectively. Only the Principal is changed. So it would be wise if you can just mug this line :
1st part : 2nd part : 3rd part = 23*24 : 22*24 : 23*22
Based on the above line, you would be able to solve such questions in a jiffy. 
But note that it will only work if the question is on Simple Interest. Like the below question appeared in SSC CGL Tier 2-

Here the data is same. i.e., R=5% and T1, T2, T3 = 2, 3, 4 years, respectively. So we will write directly –
1st part : 2nd part : 3rd part = 23*24 : 22*24 : 23*22
A received = (23*24)/ (23*24 + 22*24 + 23*22) * 7930
Answer : Rs. 2760

Q. 5) If a certain sum of money P lent out for a certain time T amounts to P₁ at R₁% per annum and to P₂ at R₂% per annum, then

 

 

 

Apply the formula:
R = (650-600)*100/600*6 – 650*4
R = 5%

Alternative Method :

 

1.44P = P(1 + r/100)^2

P(1.05^3 – 1) – 0.15P = 244
P = Rs. 32000

A = P(1+r/100)^t

Total CI = 0.05P + 0.0525P = 0.1025P

= [(1587/1200)^1/2 – 1]*100

= 15%