For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
In this article I have covered questions related to Boat and Streams, Gun-shots and some other left over topics.
Apply the direct formula
Average speed for the complete journey = 2XY/(X + Y) = 2*20*30/50 = 24 km/hr
Answer : (D)
Let the total distance be 100 km
Average Speed = Total Distance/Total Time
Total time = 70/20 + 10/25 + 20/8 = 3.5 + 0.4 + 2.5 = 6.4
Average Speed = 100/6.4 = 15.625 m.p.h
This is again a very frequently asked question. Let the distance of his school be X km.
(Time taken to reach the school at 3 km/hr) – (Time taken to reach the school at 4 km/hr) = (10 + 10) minutes or 1/3 hours
X/3 – X/4 = 1/3
Hence X = 4 km
Answer : (B)
Direct Formula
Distance = S1*S2/(S1 – S2) * Time difference
S1 = 4 km/hr, S2 = 3 km/hr, Time Difference = 10 – (-10) = 20 minutes or 1/3 hours
Distance = 4*3/(4-3) * 1/3 = 4 km
Note: In the above formula, while calculating the time difference, “late” time is written with negative sign.
Method 1
Let time taken by second runner = t. So time taken by first runner = t + 32/60 = t + 8/15
Since distance is constant, hence speed and time are inversely proportional
S2/S1 = T1/T2
16/15 = (t + 8/15)/t
16/15 = 1 + 8/15t
1/15 = 8/15t
t = 8 hours
So second runner takes 8 hours to cover the distance with a speed of 16 km/hr
Hence distance = 8*16 = 128 km
Method 2
Let the distance be X km. Then,
X/15 – X/16 = 32/60
Solve for X
X = 128 km
Answer: (A)
Method 3 (Direct formula)–
In such questions you can use the same formula you used for Q. (3)
Distance = S1*S2/(S1 – S2) * Time difference
Distance = 16*15/(16 – 15) * (32/60) = 16 * 15 * 32/60 = 128 km
A man rows down a river 15 km in 3 hrs.
Hence, Downstream Speed(v) = 15/3 = 5 km/hr
Similarly, Upstream Speed(u) = 15/7.5 = 2 km/hr
v = Rate in still water + Rate of stream
u = Rate in still water – Rate of stream
Add the above 2 equations-
Rate in still water = (v + u)/2 = (5 + 2)/2 = 3.5 km/hr
Answer: (C)
We have in the above question-
Speed of the current = (v – u)/2
u = 36/6 = 6 km/hr
v = 48/6 = 8 km/hr
Speed of the current = (8 – 6)/2 = 1 km/hr
Answer: (D)
Let the distance be X km. Let he takes ‘t’ time downstream, then he will take ‘2t’ time upstream.
Downstream speed(v) = X/t
Upstream speed(u) = X/2t
Speed of the boat in still water/Speed of the current = (v + u)/(v – u) = (X/t + X/2t)/(X/t – X/2t)
= 3/2 : 1/2
= 3 : 1
Answer : (B)
Direct formula-
So, Speed of the boat in still water/Speed of the current = (2t + t)/(2t – t) = 3 : 1
Given,
24/u + 28/v = 6 or 12/u + 14/v = 3 … (1)
30/u + 21/v = 6.5 … (2)
The best way to solve (1) and (2) is by eliminating a variable.
Multiply equation (1) by 3
36/u + 42/v = 9 … (3)
Multiply equation (2) by 2
60/u + 42/v = 13 … (4)
Subtract equation (3) from (4)
24/u = 4
u = 6 km/hr
Put u = 6 in equation (1)
v = 14 km/hr
Speed of the boat in still water = (u + v)/2 = (6 + 14)/2 = 10 km/hr
Answer: (D)
Q. 9) Two guns were fired from the same place at an interval of 13 minutes but a person in a train approaching the place hears the second shot 12 mins 30 seconds after the first. Find the speed of the train(approx) supposing that sound travels at 330 m/s.
A. 40 B. 47 C. 55 D. 60
Distance travelled by sound in 30 sec = Distance travelled by train in 12 min 30 sec
Let the speed of the train be X m/sec
Distance travelled by sound in 30 sec = 330*30 metres
Distance travelled by train in 12 min 30 sec (750 sec) = X*750
330*30 = X*750
X = 13.2 m/sec = 13.2 * 18/5 km/hr = 47.52 km/hr
Answer: 47 km/hr
Explanation
When you hear the gun shot, that means the sound has travelled to your ears.
First consider a simple scenario when the train is not moving. When the two shots are fired from A, a person sitting in the train will hear them at an interval of 13 minutes only. The sound travels the distance from A to B.
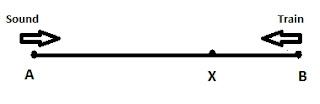
Now let us consider the scenario when the train is moving from B to A. When the first shot is fired, the sound will travel from A to B and the person sitting inside the train will hear it instantly. Now when the second shot is fired after 13 minutes, the sound would not have to travel from A to B, because the person sitting inside the train is not at B any more. He has moved from position B to X. Hence the sound only needs to travel from A to X.
Hence in this case, the person is hearing the shot after 12 minutes 30 seconds. Instead of travelling for 13 minutes (from A to B), now the sound is travelling only for 12 min 30 sec (from A to X). Hence we can say,
AB = Distance travelled by sound in 13 minutes
AX = Distance travelled by sound in 12 minutes 30 seconds
XB = Distance travelled by sound in 30 seconds … (1)
After 12 minutes 30 seconds, the sound moves from A to X and also the train moves from B to X.
BX = Distance travelled by train in 12 minutes 30 seconds … (2)
Hence from (1) and (2) we can say-
Distance travelled by sound in 30 sec = Distance travelled by train in 12 min 30 sec
Q. 10) Two guns were fired from the same place at an interval of 10 minutes and 30 seconds, but a person in a train approaching the place hears second shot 10 minutes after the first. The speed of train (in km/hr), supposing that sound travels at 330m/s is:
A. 19.8 B. 58.6 C. 59.4 D. 111.8
Distance travelled by sound in 30 sec = Distance travelled by train in 10 minutes (600 sec)
330*30 = X*600
X = 16.5 m/sec or 59.4 km/hr
Answer: (C)
I have covered almost all the type of questions that are asked by SSC from this topic.