 For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
Sine and Cosine Rules
See the image above and mug the formulas thoroughly. Sin and cosine rules are important in trigonometry and can help you in solving some complex questions.
- 1)

The figure will look something like this –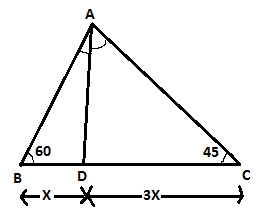
In triangle ACD
sin∠CAD/3x = sin45/AD … (1)
In triangle ABD
sin∠BAD/x = sin60/AD … (2)
Divide equation (2) by (1)
3* sin∠BAD/sin∠CAD = sin60/sin45
sin∠BAD/sin∠CAD = √6/6 = 1/√6
Answer: (C)
Similarly you can use cosine law to find any angle, if all the sides are given or to find a side, if the other two sides and an angle is given.
- 2) In the below figure, ABC is right angled at B and AD = CD. If ∠ACB=30, find ∠ABD

(A) 30 (B) 60 (C) 45 (D) 75
∠BAD = 180 – (90 + 30) = 60
In triangle ABD
sin∠ABD/AD = sin60/BD [Since ∠BAD = 60]
In triangle BCD
sin∠CBD/CD = sin30/BD
Divide equation (2) by (1)
sin∠CBD/sin∠ABD = sin30/sin60 [AD = CD and hence they will cancel out]
Now, sin∠CBD = sin(90 – ∠ABD) = cos∠ABD [convert sin into cos]
Hence, cos∠ABD/sin∠ABD = sin30/sin60
cot∠ABD = 1/√3
Hence ∠ABD = 60
Answer: (B)
Alternative Method
The figure given in this question is very important and at times it is embedded in some other figures. There is one short-cut to calculate the angle.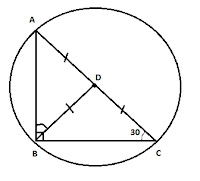
Imagine the triangle in circumscribed in a circle
Now, D will be the centre of the triangle with diameter AC. We can say with surety that AC is the diameter of the circle because ∠ABC = 90, and we know angle in a semicircle is right angle. Moreover AD = CD, hence D is the midpoint of the diameter or the centre of the circle
Now you can see that AD, CD and BD are radii of the circle. Hence AD = CD = BD
∠BAD = 180 – (90 + 30) = 60
∠ABD = ∠BAD = 60 [Since AD = BD]
Answer: (B)
Now let us see a CGL question, in which the above figure was embedded.
- 3) G is the centroid of Triangle ABC, and AG=BC. Find angle BGC.
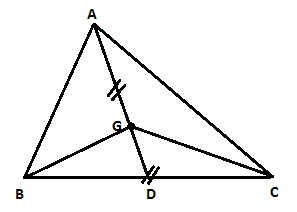
(A) 60 (B) 90 (C) 120 (D) 75
Let AG = 2x
Then BG = x (centroid divided the median in 2:1 ratio)
BC = AG = 2x
Let AG when extended cuts BC at D
Then D is the midpoint of BC (as AD is the median)
BD = DC = x [Since BC = 2x]
Now DG = BD = DC = x
That means D is the centre of a circle with diameter BC and one of the radius as DG.
Hence BGC = 90 (angle in a semi-circle)
Answer: (B)
- 4)

sec2x + tan2x = 5/3
We know, sec2x – tan2x = 1
Adding the above two equations
2sec2x = 8/3 or sec2x = 4/3
secx = 2/√3
That means x = 30
cos2x = cos60 = 1/2
Answer: (C)
Method 2:
sec2x = 4/3
That means, cos^2x = 3/4 and sin^2x = 1 – 3/4 = 1/4
cos2x = cos^2x – sin^2x = 3/4 – 1/4 = 1/2
- 5)

Multiply and Divide RHS by 2
(cosx – sinx)/(cosx + sinx) = (√3/2 – 1/2)/(√3/2 + 1/2)
Match RHS with LHS and you can easily see x = 30
Answer: (A)
Method 2
Cross multiply
(cosx – sinx)(√3 + 1) = (cosx + sinx)(√3 – 1)
Solve it and you will get, tanx = 1/√3
Hence x = 30
- 6)

Put θ = 45
2y*cos45 – x*sin45 = 0
2y = x … (1)
2x*sec45 – y*cosec45 = 3
2x – y = 3/√2
4y – y = 3/√2 [Put x = 2y]
y = 1/√2
Hence, x = 2y = √2
x^2 + 4y^2 = 2 + 4*(1/2) = 2 + 2 = 4
Answer: (C)
Some important values to mug:
- sin15 = (√3 – 1) /2√2
- cos15 = (√3 + 1) /2√2
- tan15 = 2 – √3
- cot15 = 2 + √3
These values are very important to solve some tricky trigonometric questions. Examples :
- 7)

Although you can solve this question with the direct formula, which I discussed in Geometry Tricks – 1. But let us assume, you forget that formula. In such cases, the values of sin15 and cos15 will come handy.
Let the perpendicular and base of the triangle be P and B, respectively.
sin15 = Perpendicular/Hypotenuse = P/100
P = sin15*100
Similarly, B = cos15*100
Area = 1/2 * P * B = 1/2 * sin15 * 100 * cos15 * 100 = (√3 – 1) /2√2 * (√3 + 1) /2√2 * 100 * 100/2
Area = 100*100/8 = 1250
Answer: (D)
- 8)

A) 0 B) 1 C) -1 D) 2
Put x = 15
= cot15/(cot15 – cot45) + tan15/(tan15 – tan45)
= (2+ √3)/(1 + √3) + (2 – √3)/(1 – √3)
= 1
Answer: (B)
Some candidates are asking me the book which I refer to write these articles. But, I can assure you that all these tricks are authored by me and you won’t find them in any book or coaching…
If you have any doubt in this article, please drop a comment…
Keep Reading 🙂








