 For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
Algebra is the easiest topic for SSC because you don’t have to memorize any formula for it and all the questions can be solved within 10 seconds with jugaad.
First let me share with you the concept of symmetrical expressions(as I call it). A symmetrical expression is the one in which the weight of all the variables (a, b, c, etc.) is equal. Examples will make things clear.
Examples of symmetrical expressions –
- a3 + b3 + c3
- 3a + 3b + 3c
- a2 + b2 + c2
- a + b + c
- ab + bc + ca
Examples of non – symmetrical expressions –
- a – b + c
- 2a + 3b + 3c
- a3 + b2 + c3
- a + b + c2
Hack – 1 : “Whenever you encounter a symmetrical equation in any question, you can safely assume : a = b = c (even if it is not given in the question)”
Let’s solve previous year questions –
Q . 1.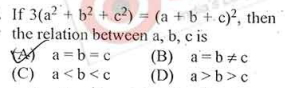
Here you can see that the LHS as well as the RHS of the equation is symmetrical, hence a = b = c
Answer : (A)
Q .2. 
We put a = b = c, hence (a+c)/b becomes (a+a)/a, or 2
Answer : (B)
Q . 3.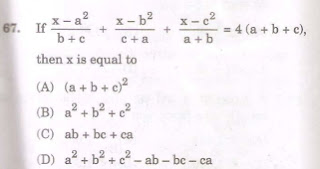
In this question we have to find the value of x.
Here the equation is completely symmetrical, hence we assume a = b = c
Put b=a, c=a (so that the whole equation is in terms of ‘a’)
Now LHS becomes 3(x – a2)/2a
RHS = 12a
Solving this, you will get, x = 9a2
From here we get that the value of x is 9a2
Now put a = b = c in all the 4 options and check which option gives you the value 9a2
A) 9a2
B) 3a2
C) 3a2
D) 0
Answer : (A)
Q . 4. 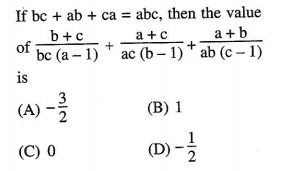
bc + ab + ca = abc is symmetrical and hence we can assume a=b=c
Now put b=a and c=a in this equation. We will get –
3a2 = a3
So a = 3
Now put a=b=c=3 in the expression whose value we have to find. You will get the answer as 1.
Answer : (B)
Hack – 2 : “When only a single equation is given and based on that you have to find the value of an expression, you can assume the value of variables yourself. But make sure to assume only such values that will not make the denominator zero”
Examples :
Q . 5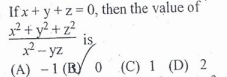
In this question, only a single equation is given, i.e., x + y + z = 0, and based on this equation we have to find the value of an expression
We can assume x = -1, y = 1 and z = 0 (such that x + y + z = 0)
Now on putting these values in the expression, we get the answer as 2
Answer : (D)
Q . 6. 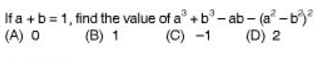
a + b = 1
Let’s assume a = 1 and b = 0
Put the values in the expression, and you will get 0.
Answer : (A)
Q . 7.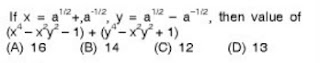
In this question the values of x and y both depend on a constant ‘a’. We can assume any value for ‘a’ and this will give the values of x and y. Let us assume a=1
This will give x = 2 and y = 0
Put these values in the expression and you will get the answer as 16.
Answer : (A)
Q . 8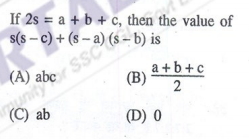
Pick values for a, b and c, such that their sum is 2s. Let us assume a = 2s, b = s and c = -s (here you should not assume a,b or c to be zero because that will make the elimination of options difficult)
Put these values in the expression and you will get 2s2
Now check all the four options to see which of them will give the value 2s2 on putting a=2s, b=s and c=-s
Answer : (C)
Don’t forget to read Algebra Tricks – 2, 3 and 4












