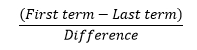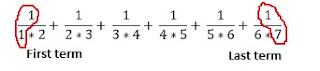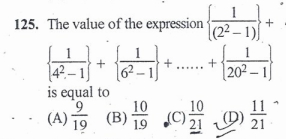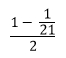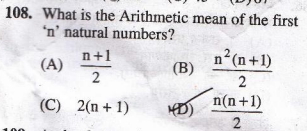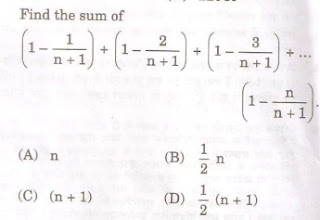For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
There are basically two types of questions that are asked by SSC from this part-
1. Finite sequence where the denominator is of the type 1×3, 3×5, 5×7, etc. (can be solved with direct formula)
2. An infinite sequence where you have to find the series (the sum of infinite sequence)
First of all let’s see questions of type 1.
Q.1) 1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42
First break it into the required form-
Now apply the direct formula-
Difference is the gap between the two numbers in the denominator. So here difference = 2-1 = 1
Answer : 6/7
Next question
Again break it into the required form-
1/3 + 1/15 + 1/35 + … + 1/399
= 1/(1*3) + 1/(3*5) + 1/(5*7) + … + 1/(19*21)
Apply the formula
Answer : 10/21
Now let us move to the second type of questions where we will be applying the real tricks-
To begin with, I have taken the most basic question. Although many of you might be knowing that the sum of first n natural numbers is n(n+1)/2 and hence the arithmetic mean of first n natural numbers will come out to be (n+1)/2
But let’s say you forget the formula (exam pressure) and you can’t recall it. What will your approach be?
The trick is simple- suppose a value of ‘n’.
‘n’ defines how many terms from the sequence you are taking
Let us take n = 2
Arithmetic mean of first 2 natural numbers = (1+2)/2 = 3/2
Now put n = 2 in all the four options and check which option is giving 3/2 as the output
A) 3/2
B) 6
C) 6
D) 3
Answer : (A)
But till now we have killed only a mouse, let us go and catch some lions.
I will take n = 1 (you can take n = 2 as well but that will make the calculations a little complex in this question). But I will solve this question by taking n = 1 and n = 2 both, so that you become well-versed with the concept.
n = 1
Sequence will reduce into (1 – 1/(n + 1))
Put n = 1
Value = 1/2
Now put n = 1 in all the four options and check which one of them is giving 1/2 as the output
A) 1
B) 1/2
C) 2
D) 1
Answer : (B)
Now n = 2
Sequence will reduce into (1 – 1/(n + 1)) + (1 – 2/(n + 1))
Put n = 2
Value = 2/3 + 1/3 = 1
Now put n = 2 in all the four options and check which one of them is giving 1 as the output
A) 2
B) 1
C) 3
D) 3/2
Answer : (B)
Remember in the exam you will take either n = 1 or n = 2, I have taken both just to explain you the concept. But in some questions you may find that after taking n = 1, you are getting two options with the same value. In such cases you will have to take n = 2.
Let me take some questions of ‘Averages’ in this article itself. Firstly an easy one –
Assume the numbers as 1, 2, 3, 4 and 5
Average of these numbers = 3
Include the next two numbers (6 and 7)
Average of 1, 2, 3, 4, 5, 6, 7 = 4
Average has increased from 3 to 4
Answer : (A)
Now a tougher one –
This question appeared in Tier 2 (2015). It talks about average and hence it would be wise to at least take n = 2 or n = 3. Let us take n = 2.
It is given that ‘Average of n numbers is a’ and no other information is given, so you can assume the numbers as well. Since you have assumed n = 2, so you will have to assume two numbers. Let me take 1 and 3 as the two numbers (note : you can take any two numbers you want).
Average of 1 and 3 = 2
Hence a = 2
First number is increased by 2 and second number is increased by 4. Hence 1 and 3 will become 3 and 7.
Average of 3 and 7 = (3 + 7)/2 = 5
Now put a = 2 and n = 2 in all the four options and check which one of them is giving 5 as the output.
A) 5
B) 3.5
C) 7
D) 5.5
Answer : (A)
I hope the concept is clear now…